Doing head counts is a skill we are losing over time, and this no one can disagree with. We are much worse at doing accounts than our parents, for example, since they were trained for the task at a time when there was no extra resource that would facilitate mathematical processes. Already, we have a partner that solves all the hard work in milliseconds: the calculator.
The basic configuration of the device is simple. 10 numbers buttons, 4 operation buttons and 1 button to display the calculation result. Just press the desired key sequence and that’s it, the result comes out right. Anyone who doubts can do it on hand to confirm, if you can, of course.
But have you ever stopped to think about what goes on in there and make the calculations run correctly? Yeah, I already did. The answer gave a post, check it out.
How we got in pocket calculators
As you may suspect, all the magic comes from a small component embedded in the calculators called an integrated circuit, or, MICROCHIP , as it is popularly known. But I can not just come here and dump the theory, especially since the calculators have a rather interesting story. I take this opportunity to tell you now.
Mechanism of Anticítera: The computer of 2000 years
Well, first I emphasize one point: it is not that there were no calculators before the microchips, after all we had the abacus for millennia and many other examples of mechanical machines that make calculations in the history of science, but they were slow, rare and susceptible to errors, many errors, after all, their outcome depended on how the intermediate steps were operated by humans. That’s right, too, but the error rate between tightening plastic buttons and setting and rotating cranks changes drastically.
This is why we often divide the history of calculators between “before electronic calculators” and “after electronic calculators”.
And the first of the electronic calculators came well before the microchip came up and was called ENIAC, which I do not think you would enjoy having in your house. ENIAC was 1,000 times faster than electromechanical calculators and could contain a decimal number of up to ten digits in memory. This was very advanced for the 1940s, but this breakthrough had a price (and a size): 17,468 valves, 7,200 crystal diodes, 1,500 relays, 70,000 resistors, 10,000 capacitors, and about 5 million hand-welded joints. It weighed about 27 tonnes, occupied 170 square meters and consumed as much energy as a small town.
Everything that appears there is just a little bit of ENIAC
Of course ENIAC was not intended for the masses, since it was a government computer, but the bases for the modern calculation were launched with it, and therefore the continuity of the research and miniaturization of the components would give life to the transistors. So the gigantic valves used in the ENIAC, which could measure up to 30 centimeters each, would be replaced by tiny components capable of creating a calculator small enough to fit on an office desk.
Created in 1947, the new transistors could be allocated in thousands on a single plate less than 5 square centimeters (today, BILLIONS of transistors fit in the area of a human nail, for example). Transistors were the key to the success of the new technology that came up, were cheaper, simpler to produce, much smaller, faster and did not even heat up.
The ANITA of the 60’s
The first model of this new era for calculators arose in 1961 in England and was called ANITA, an acronym for A New Inspiration To Arithmetic Accounting (or, A New Inspiration for Arithmetic / Accounting). But there was still a problem: Price. At its launch an ANITA cost between 350 and 400 pounds, which gives almost $ 9,000 in current money.
So you can imagine that they came to be very common, right? But we’re getting there. The answer to ANITA’s problem, even, had even been invented the day of its launch.
It was not long before transistor research advanced to the point of combining them into large groups to optimize results. And what is the name of a bunch of transistors heaped up in a single plate in order to optimize a particular process? That’s right, microchip .
The microchip came in the late 1950’s and is nothing more than a board that combines several groups of transistors and capacitors. So it can be more efficient in a much smaller space of hardware than previously had. Jack Kilby, of Texas Instruments, decided that with his help it was possible to cheapen, reduce, and popularize the personal calculator (and make a lot of money with it, clear).
The first – and still rather rudimentary – integrated circuit presented in 1958 at Texas Instruments
So in 1967 they released Cal Tech a more portable version (about 1 kg) costing only “$ 150” (just over $ 1,100 in current values) and doing the 4 basic math operations and could still print the result in a little ribbon. The company sold calculators like no one else and helped popularize the technology. Soon more and more everyday products would be optimized by microchips.
From the price of over a thousand dollars to $ 1.99 and the weight of 1 kg to a few grams that fit in your pocket, it was a jump.
The legendary Cal Tech
Okay, now that we know how we got here, we can already understand to move on to the theoretical part and understand how microchips operate the miracle of calculating 51651 times 218541 in milliseconds.
The history of Silicon Valley
PS The same Texas Instruments had already created the first pocket radio to replace the valves with transistors more than 10 years before the launch of Cal Tech. All these revolutions were conducted in Silicon Valley, and you can check in an exclusive post by clicking on the square on the side.
The basis of a calculator (and all electronics)
Ok, the microchip leaves the process of doing mathematical operations faster, BUT HOW? Calm down, before you close this page because we’re taking too long to get to the main subject, I’ll start by explaining the process.
Initially you need to keep in mind a clear concept in your head: Everything in computing revolves around 0s and 1s, the famous binary language. Everything.
So when you are using the computer and type Google in the browser, what is actually processed is 01100111 01101111 01101111 01100111 01101100 01100101 , where each of these 8-digit groups represents a letter. In addition, the browser itself and what is displayed on it is running in a sequence of 0 and 1 different.
Quantum Computers: The Future of Computing
As said there in the subtitle, 10 lines above, that is the basis of electronics. so it also works for the numbers entered in the calculator. In this language the digit 1 will be 00000001, the number 2 will be 00000010, the 3 will be 00000011 and so on.
And if you’re wondering why binary language exists or why binary language only has 2 states (0 and 1), here’s the answer: Remember the transistors we talked about earlier? Everything revolves around them.
As you know, the computer (or its pieces, like processor, memory, etc.) are inanimate things that do not think. Even if we pass the binary language to them, they will not understand the 0s and 1s; they do not know how to interpret this, they do not know that a zero is a zero. But there is one thing they know and understand well: electricity.
Thus, the transistors act like small “switches” of metal that serve to let pass the electric current, or not to let pass the electric current. If the current passes through transistor A something happens, if not pass happens another. Now multiply that by a few billion (number of transistors in your machine’s processor, probably) and you’re ready to run the computer; whether it’s running a game, watching a video, or editing a photo. Everything is binary. Crazy, right?
Ahh, and explaining why it’s only 0 and 1: The reason is that electricity has only 2 stages. Either it is on or off. Score.
I should not be opening this parenthesis here, as this may complicate, but it will: a new revolution is about to happen and everything you’ve read so far is about to change.
As we approach the maximum limit of transistors embedded in a chip ( read more about Moore’s Law by clicking here ), the number of quantum computers in operation increases. Strange as it may seem, a quantum computer does not operate through binary language, as they have 3 states and not just 2. Instead of the electric current being connected or not (as would be normal), here it can be turned on, off or the 2 at the same time !!
The thing is bizarre, I know, but I will not go into this subject here in this post since it would require a full post on the topic to deal with all its possibilities. But look how lucky: This post already exists: D If I were you I would click here to read right now about quantum computing and how it will change everything in our lives .
As the bits turn up numbers and the calculations are made
If you have understood this far, without mysteries, you are close to understanding how a calculator operates at its lowest level.
Briefly, the scheme is as follows: As soon as you enter the button corresponding to the number 2, the binary 00000010 goes to memory. When you press the sum button, the microchip indicates that it must perform a sum of values and, as soon as the second value is inserted, let’s say it is the 00000011, also known as 3, the result of the operation, 00000101, will be sent to the display, which makes the process inverse, turns it into decimal and shows the 5.
The methods of addition, subtraction, division and multiplication each work in their own way, with a different combination of logical gates and the help of an adder (or arithmetic circuit, but no one uses that non-translated name). Let’s see how important they are in the process.
Logical doors
Logical ports are devices that receive infinite inputs and produce a single output , these outputs being “true” or “false”. That simple. The configuration to operate a sum will be one, the configuration to generate a division is another, etc.
There are 7 different logic gates, but we’ll just need to understand the 4 basic gates to figure out how a calculator works. Are they:
- AND gate : “And” means “E”, ie if the input values are the same , the output is true. Anything other than this will result in false.
- OR gate: Or the “Or” in English, means “or”. So, for the output to be true, at least one of the inputs must be true.
- XOR port: The “Xor” port, which comes from “exclusive or” or “exclusive”, only generates true output if the input values are different.
- PORT NOT: Lastly the “Not” port which means “no”. It is the simplest of all because it only reverses the input value. If received true as input then the output will be false and vice versa.
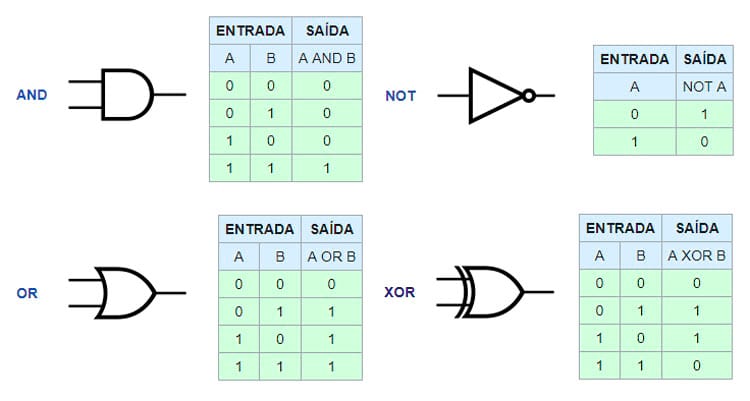Representation of each port and its truth table, that is, the values that come in and how they come out. Note that in computing, 0 is FALSE and 1 is TRUE.
Adders
But only the logic gates do not give the message, after all, the operations will always result in an “extra digit”. To illustrate, let’s remember there from the second series, when you would add 15 and 25, for example.
At that time you did not do the head calculation and then did the process according to the costume: put one number over the other and then began to add from right to left. First it added 5 of 15 with 5 of 25. The result is 10, then 0 goes down and 1 “rises” to be added with the values on the left, in this case 1 and 2, right? Well, this 1 being carried between calculations is the function of adder in a binary operation.
Notice that in binaries we only have 2 possibilities: 0 or 1. And adding the torque 1 with another torque 1 already exceeds the limit of possibilities. So in this case the result is 0 and a 1 is loaded to be embedded in the next operation on the left. This 1 that “rises” in binary operations is called “carry”, which comes from the English “load”. The GIF below shows a binary sum happening.
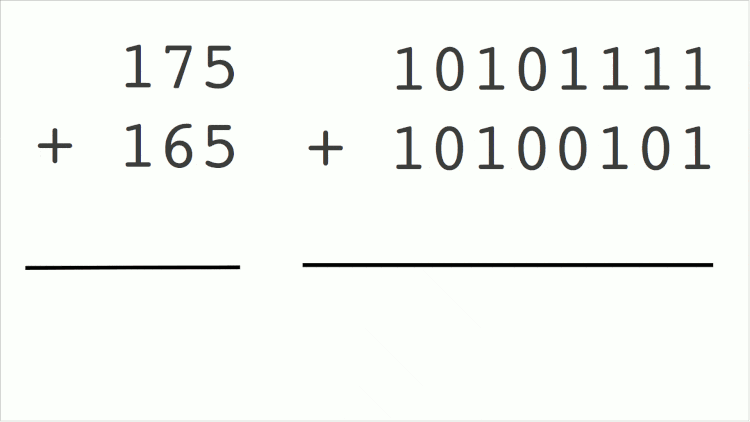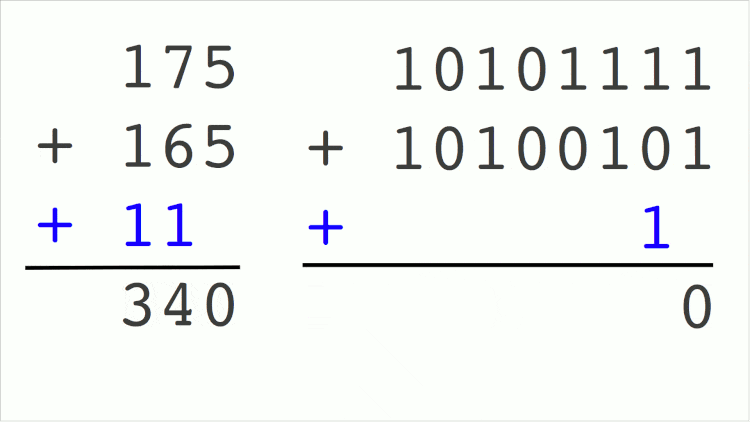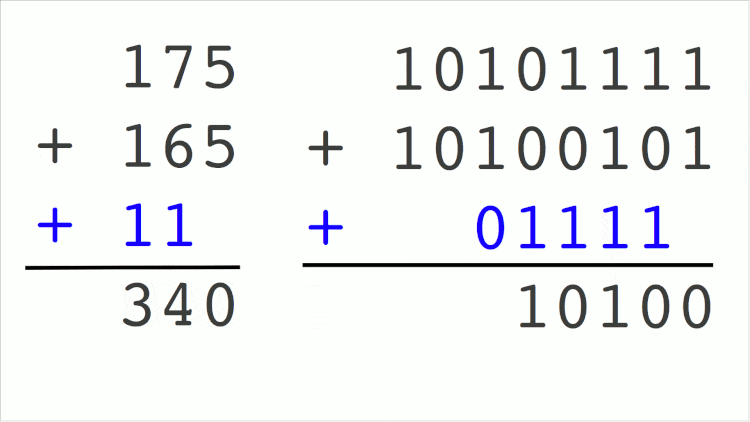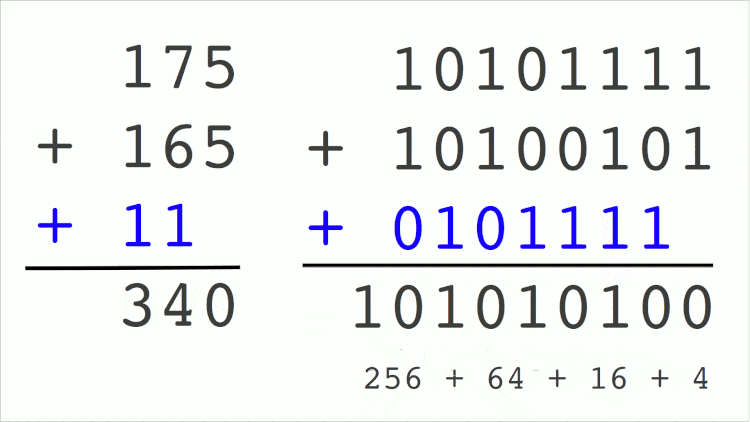The same sum being made the way we know it (decimal mode) and the way computers know (binary). The numbers in blue are the “remainder” values in the calculation that go up – even though they are descending in this GIF
The adders exist in two forms: Full adder and half adder, being this second the most used and most common in the examples that we will see below, soon.
Now just get everything, mix different combinations between these four logic gates with a half adder and you will have a device capable of doing calculations. Understood the theory, we can go to the examples of logic circuits, but rather an important observation: the circuits below are NOT THE ONLY OPTION to do the operations . Things can vary greatly depending on the complexity of the calculator, size of the hardware, etc. etc.
Sum of binaries
Because it is the most common operation, I will explain the sum of binaries in more detail, with all the necessary step by step. The others will be explained without so much “coaxing”.
Going back to the truth tables seen above, let’s take the Xor logic gate, which is the basis of a sum operation, and apply the concept of carry, that is, the “number that goes up.” Thus the possibilities of a xor port applied to the sum of torque are as follows:
- 0 and 0 results in 0;
- 0 and 1 results in 1;
- 1 and 0 results in 1, and
- 1 and 1 results in 0 with a 1 going to the next leftmost sum
Soon, it will be represented in the way you see below, already counting on the carry (or adder) to work with the number that goes up.
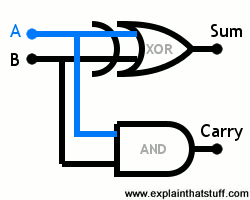
In the example to the side we are inserting two binary numbers to be added (A and B). They “travel” simultaneously to the inputs of the two logic gates – one xor port at the top and one and down port that works as adder. The output of the xor port gives the sum of the two inputs, while the output of the and port tells us whether we need to raise a 1 or not. then the process is repeated until there are no more binaries to be added and the final value is obtained.
To get more we will get the four possibilities of output from a xor port and simulate an output :
- If A and B get a zero, we are making the sum 0 + 0 = 0. So the xor port will result in zero and the and port as well (remember that to output port 1 and you need the two inputs to be 1 ). So in this case the result of our sum is zero and carry is also zero.
- If A receives a 0 and B receives 1, we are making the sum 0 + 1 = 1. The xor port gives 1 if either (but not both) of its entries is 1. Port and gives 1 only if both entries are 1. Then the result of our sum is 1 and the carry is zero.
- If A receives 1 and B receives 0, it is the same as in the previous example: the result of our sum is 1 and the carry is 0.
- Finally, if A and B receive 1, we are making the sum 1 + 1 = 2. Now the xor port gives 0, while the and port gives 1. Therefore, the sum is 0 and the carry is 1, which means that the end result is 10 in binary or 2 in decimal.
Subtraction of binaries
To do a subtraction the process is similar to the sum, but it has an additional element of paramount importance: the not port .
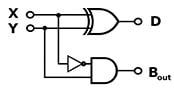
The secret of subtraction is not
One way to assemble the circuit can be seen on the side. In this model a half-adder was used, thus assembling a simpler but more limited circuit. Note that it is possible to calculate X – Y, but it is not possible to calculate Y – X. All because it is not present on one side of the operation.
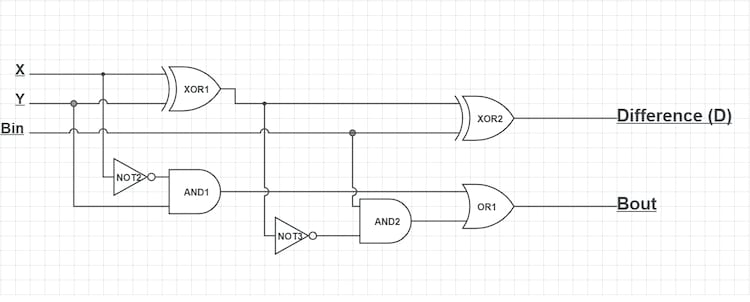
To solve this could be used a full adder, which would leave the process more complex, as you can see below.
Multiplication of binaries
Already with the multiplication will be done as follows: Let’s say that our account is 8 times 14. In binary the 8 is 1011 and the 14 is 1110 . Thus, to multiply 1011 by 1110 we will take the number from above (1011) and multiply by each digit from 1110, from right to left.
- 0 times
- 1011 times 1
- 1011 times 1
- 1011 times 1
The results are placed one below the other, moving a house to the left with each new value. And to generate these results has no mystery no. Just multiply normally. When multiplied by 0 the result is 0 and when multiplied by 1 is 1. Simple. Here’s an example of how it works in practice.
In practice, if the multiplication is by 0 you put 0 across the line, if it is 1 you copy the line that is being multiplied the same
In the end a sum of binaries is done, just as we make a sum after executing the multiplication of the digits in our traditional decimal mode that we learned in school. Multiplication, by the way, is the easiest and similar method to what we are accustomed to.
One of the possible circuits for multiplication can be seen below, where 2 values of 2 bits each are multiplied.
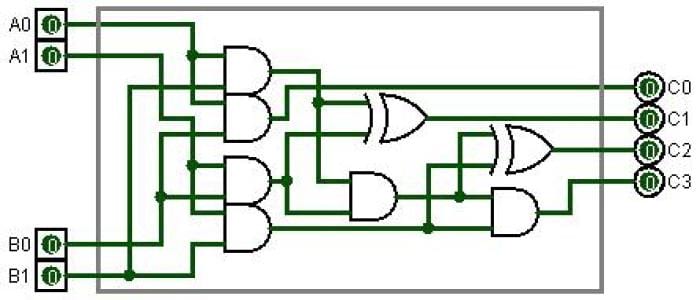
Division of binaries
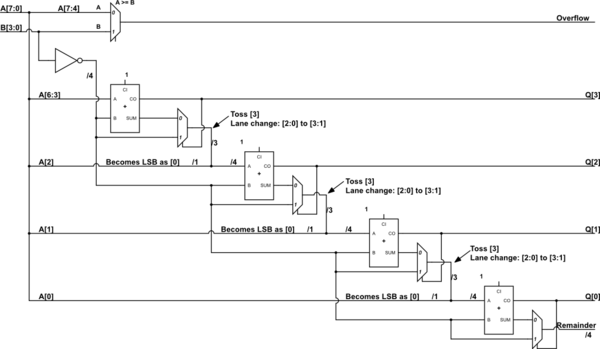
And to close, the division of binaries happens in a similar way to the decimal mode, with the difference that you should pay attention to how you subtract when you clear the rest of the division, since you need to use the subtraction of binaries, of course.
One of the possible logical circuits for a division would be:
Well, unless you’re taking a course in electronics, engineering, or computer science, here’s a good foundation on how a calculator works. In short: Everything is done from a number of logical gates AND, OR, XOR and NOT contained within chips that are connected to each other. Arrange all this on a board and you will have a calculator.
PS I reaffirm: Of course we can use other circuits, including other logic gates, but delving into this topic is up to anyone who has an interest. If this is your link, below are good links.